Product Of Inertia Calculator

Mass 1 (m₁):
Distance from x-axis (x₁):
Distance from y-axis (y₁):
Mass 2 (m₂):
Distance from x-axis (x₂):
Distance from y-axis (y₂):
Mass 3 (m₃):
Distance from x-axis (x₃):
Distance from y-axis (y₃):
Calculate Result:

Introduction

Calculating the product of inertia is essential in various engineering and physics applications. It helps determine how mass is distributed in a rigid body relative to its axis of rotation. This article provides a simple and accurate calculator along with an explanation of its usage and underlying formula.

How to Use

To use the product of inertia calculator, follow these steps:

1. Input the values of mass (m), distance from the x-axis (x), and distance from the y-axis (y).
2. Click the “Calculate” button to obtain the result.

Formula

The formula for calculating the product of inertia (Ixy​) is given by:

Ixy​=∑m×(x×y)

Where:

• m is the mass of each element.
• x is the distance of each element from the x-axis.
• y is the distance of each element from the y-axis.

Example Solve

Suppose we have three masses distributed in a plane:

• Mass 1 (m1​) = 2 kg, x1​=3 m, y1​=1 m
• Mass 2 (m2​) = 3 kg, x2​=2 m, y2​=4 m
• Mass 3 (m3​) = 1 kg, x3​=5 m, y3​=2 m

Using the formula, we can calculate the product of inertia as follows:

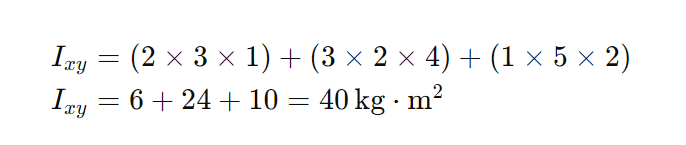
Therefore, the product of inertia (Ixy​) for this system is 40 kg·m².

FAQs

Q: What is the significance of the product of inertia?

A: The product of inertia represents how mass is distributed in a rigid body relative to its coordinate axes. It is crucial in analyzing the rotational motion and stability of structures.

Q: Can the product of inertia be negative?

A: Yes, the product of inertia can be negative. It indicates an asymmetric distribution of mass relative to the coordinate axes.

Q: How does the product of inertia differ from the moment of inertia?

A: While the moment of inertia measures an object’s resistance to rotational motion about a specific axis, the product of inertia describes the distribution of mass relative to two perpendicular axes.

Conclusion

The product of inertia calculator provides a convenient tool for engineers and physicists to analyze the distribution of mass in a rigid body. By understanding its usage and formula, users can accurately determine the product of inertia for various applications.