Bending Strength Ratio Calculator
Introduction
In engineering and material science, determining the bending strength ratio of a material is crucial for designing structures capable of withstanding loads. With the aid of modern technology, calculating this ratio has become easier than ever. In this article, we’ll delve into the process of using a bending strength ratio calculator, providing a step-by-step guide along with a working example.
How to Use
Using the bending strength ratio calculator is straightforward. Simply input the required parameters, such as the modulus of elasticity (E), moment of inertia (I), and applied load (F). Once these values are entered, click the “Calculate” button to obtain the bending strength ratio.
Formula
The bending strength ratio (σ) can be calculated using the formula:
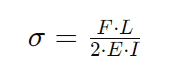
Where:
- σ = Bending strength ratio
- F = Applied load
- L = Length of the beam
- E = Modulus of elasticity
- I = Moment of inertia
Example Solve
Let’s consider an example where:
- Applied load (F) = 500 N
- Length of the beam (L) = 2 m
- Modulus of elasticity (E) = 200 GPa
- Moment of inertia (I) = 0.05 m^4
Substituting these values into the formula:

FAQ’s
Q: What is the significance of the bending strength ratio?
A: The bending strength ratio indicates the material’s ability to withstand bending stress. It’s crucial in structural design to ensure safety and reliability.
Q: Can this calculator handle different units?
A: Yes, as long as consistent units are used for all inputs, such as Newtons for force, meters for length, and GigaPascals for modulus of elasticity.
Q: Is there a limit to the size of input values?
A: No, the calculator can handle a wide range of input values, but it’s essential to ensure accuracy by using appropriate precision.
Conclusion
In conclusion, the bending strength ratio calculator provides a convenient tool for engineers and designers to assess the structural integrity of materials under bending stress. By following the simple steps outlined in this article, users can efficiently determine this critical parameter, ensuring the reliability and safety of their designs.