Stokes Law Calculator

Radius of the object (m):
Density of the object (kg/m³):
Density of the fluid (kg/m³):
Dynamic viscosity of the fluid (Pa·s):
Calculate

Introduction

Welcome to our Stokes Law Calculator! This tool is designed to help you easily calculate the terminal velocity of a spherical object falling through a viscous fluid. Stokes’ law, formulated by Sir George Gabriel Stokes, describes the drag force experienced by a small sphere moving through a viscous fluid. By inputting the necessary parameters, you can quickly determine the terminal velocity of the object.

How to Use

Simply input the values of the parameters required for calculation into the designated fields. Once you’ve entered the necessary information, click the “Calculate” button to obtain the result.

Formula

Stokes’ law is represented by the equation:

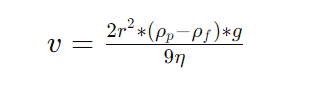
Where:

• v is the terminal velocity of the object (m/s)
• r is the radius of the spherical object (m)
• ρp​ is the density of the object (kg/m³)
• ρf​ is the density of the fluid (kg/m³)
• g is the acceleration due to gravity (m/s²)
• η is the dynamic viscosity of the fluid (Pa·s or N·s/m²)

Example Solve

Let’s calculate the terminal velocity of a spherical object with a radius of 0.05 meters, density of 1000 kg/m³, falling through water with a density of 997 kg/m³ and a dynamic viscosity of 0.001 Pa·s.

Calculation:

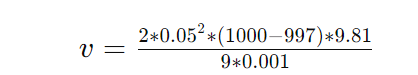
Result:

v≈0.015m/s

FAQs

Q: What is Stokes’ law?

A: Stokes’ law describes the drag force experienced by a small sphere moving through a viscous fluid.

Q: What are the units of dynamic viscosity?

A: Dynamic viscosity is typically measured in Pascal-seconds (Pa·s) or Newton-seconds per square meter (N·s/m²).

Q: Can Stokes’ law be applied to all shapes of objects?

A: No, Stokes’ law is specifically applicable to small spherical objects moving through a fluid.

Q: Is Stokes’ law accurate for all situations?

A: Stokes’ law is most accurate for small spheres moving at low Reynolds numbers in highly viscous fluids.

Conclusion

Our Stokes Law Calculator provides a convenient way to determine the terminal velocity of spherical objects in viscous fluids. By utilizing the formula and inputting the necessary parameters, you can quickly obtain accurate results.