Partial Correlation Calculator
Introduction
In the realm of statistical analysis, understanding the relationship between variables is crucial. One important measure in this regard is partial correlation, which quantifies the degree of association between two variables while controlling for the influence of other variables. To facilitate this calculation, a partial correlation calculator proves to be invaluable. In this article, we’ll delve into the functionality of such a calculator and provide a practical implementation.
How to Use
To utilize the partial correlation calculator, follow these steps:
- Input the required data into the designated fields.
- Click the “Calculate” button to obtain the partial correlation coefficient.
- Review the result displayed on the screen.
Formula
The formula for computing partial correlation coefficient (rxy.z) between variables x and y while controlling for variable z is given by:
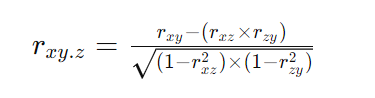
Where:
- rxy represents the correlation coefficient between variables x and y.
- rxz represents the correlation coefficient between variables x and z.
- rzy represents the correlation coefficient between variables z and y.
Example Solve
Let’s consider a scenario where we want to compute the partial correlation between variables x and y while controlling for variable z. Assume:
- rxy=0.6
- rxz=0.4
- rzy=0.7
Plugging these values into the formula:

FAQ’s
Q: What is partial correlation?
A: Partial correlation quantifies the relationship between two variables while controlling for the influence of other variables.
Q: Why is partial correlation important?
A: It helps to discern the unique relationship between variables, excluding the confounding effects of other variables.
Q: How does the calculator handle missing data?
A: The calculator assumes complete data. Missing values may yield inaccurate results.
Conclusion
A partial correlation calculator is a valuable tool for analyzing the relationship between variables in a controlled manner. By accounting for the influence of other variables, it provides insights into the unique association between two variables. Whether in research, data analysis, or decision-making processes, understanding partial correlation enhances statistical comprehension and informs better decisions.