Leibniz Rule Calculator
Introduction
In the realm of calculus, the Leibniz Rule stands as a powerful tool for computing derivatives of integrals involving parameters. Its application extends to various fields like physics, engineering, and economics. Leveraging the Leibniz Rule can simplify complex calculations, providing a streamlined approach to solving problems.
How to Use
To utilize the Leibniz Rule effectively, follow these steps:
- Identify the integral containing a parameter that needs differentiation.
- Apply the Leibniz Rule to compute the derivative of the integral.
- Substitute the values of the parameters into the resulting expression to obtain the final result.
Formula
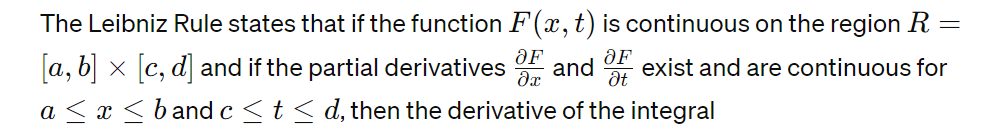

with respect to x is given by:
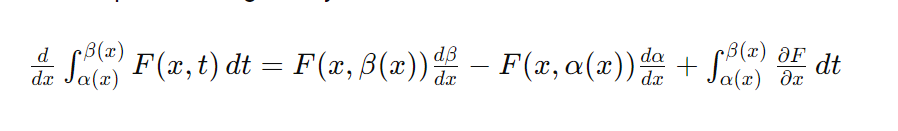
Example Solve
Let’s consider the following integral:




=C

FAQs
What are the applications of the Leibniz Rule?
The Leibniz Rule finds applications in various fields such as physics, engineering, economics, and more, particularly in solving problems involving parameterized integrals.
Is the Leibniz Rule applicable to all types of integrals?
The Leibniz Rule is applicable to integrals where the limits of integration are functions of a parameter, making it versatile for a wide range of problems.
Can the Leibniz Rule simplify complex calculations?
Yes, by allowing the differentiation of integrals with respect to parameters, the Leibniz Rule offers a systematic approach to solving complex problems, thus simplifying calculations.
Conclusion
The Leibniz Rule serves as a valuable asset in the calculus toolkit, enabling the differentiation of integrals with respect to parameters. Its versatility and effectiveness make it indispensable in various fields, offering a systematic method to tackle intricate mathematical problems.