CAPM Capital Asset Pricing Model Calculator
Introduction
The Capital Asset Pricing Model (CAPM) is a widely used financial model that helps investors calculate the expected return on an investment based on its risk and return characteristics. Implementing the CAPM in practice involves several steps, including determining the risk-free rate, the market return, and the asset’s beta coefficient. While the CAPM formula may seem complex, using a calculator can simplify the process significantly.
How to Use
To use the CAPM calculator, simply input the required values into the designated fields and click the “Calculate” button. The calculator will then compute the expected return based on the provided inputs.
Formula
The CAPM formula is as follows:
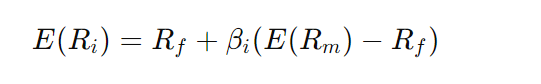
Where:
- E(Ri) is the expected return on the investment
- Rf is the risk-free rate of return
- βi is the beta coefficient of the investment
- E(Rm) is the expected return of the market
Example Solve
Let’s say we have the following inputs:
- Risk-free rate (Rf): 3%
- Beta coefficient (βi): 1.2
- Expected return of the market (E(Rm)): 10%
Using the CAPM formula, we can calculate the expected return on the investment:
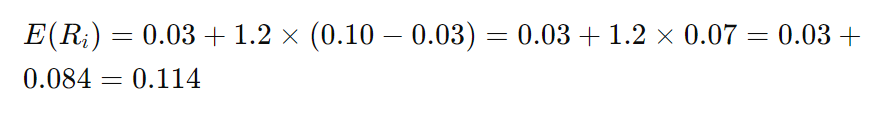
So, the expected return on the investment is 11.4%.
FAQs
Q: What is the risk-free rate?
A: The risk-free rate refers to the return on an investment with zero risk, typically represented by government bonds.
Q: What is beta coefficient?
A: Beta coefficient measures the volatility of an investment relative to the market. A beta of 1 indicates the same volatility as the market, while a beta greater than 1 implies higher volatility.
Q: How accurate is the CAPM model?
A: The CAPM model provides a theoretical framework for estimating expected returns but may have limitations in real-world applications due to assumptions such as efficient markets and linear relationships.
Conclusion
The CAPM calculator simplifies the process of determining expected returns on investments, helping investors make informed decisions based on risk and return considerations.
